Estrategias para resolver Sudokus
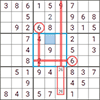
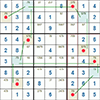
Se presentan los métodos y técnicas más comunes que se utilizan para resolver sudokus. Se centran en cómo ubicar los números por medio de la lógica para encontrar la solución.
Estrategias y métodos son necesarios para resolver los sudokus más difíciles. Se centran en el uso de los números candidatos y cómo poder eliminarlos para lograr la solución.